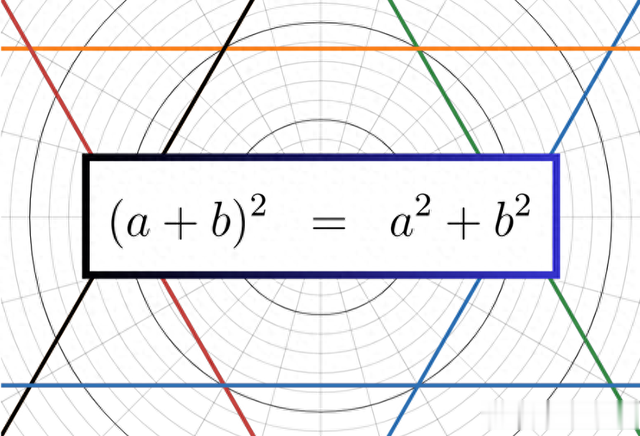狠狠干

假定 ( a + b )² = a² + b²是一个常见的数学失误。淌若你莫得想过扩大括号，这个谜底可能看起来很天然。一朝你被“你忘了 2 ab ”打断，你就会记着这个谜底。

咱们的主张是找到a和b的值，使这个不正确的等式施行上是正确的。淌若咱们像平淡通常假定a和b是数字，那么有一些情况劣等式开拓，但它们很败兴。

行动又名代数爱好者，我在学习历程中遭受过很多使这个等式开拓的独到设施，但咱们必须对a和b作念出一些篡改……

基础常识

为什么 ( a + b )² = a ² + 2 ab + b ²？除了扩大括号以外，底下是求a + b平方时发生的情况的图表：

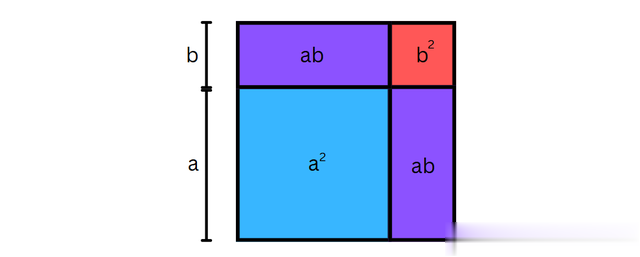
紫色矩形给了咱们独特的 2 ab。由于移除紫色矩形后体式不再是正方形，因此您可能依然唐突看到 ( a + b )² = a ² + b ² 的解。

让咱们来学习一下代数。

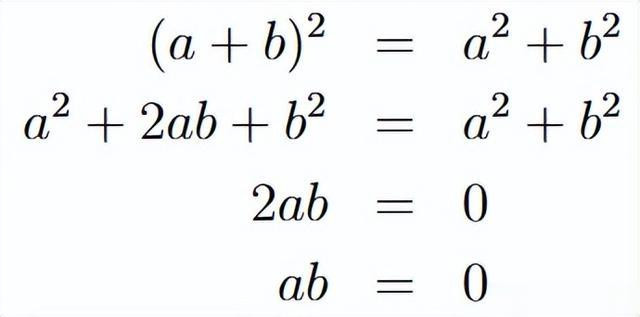
为了使等式开拓，咱们需要ab = 0，当且仅当a = 0 或b = 0（或两者）时，该等式才为真。

天然这很有劝服力，但这是基于a和b是数字的（透顶合理的）假定。让咱们略微篡改一下步调，篡改a和b 的取值。这么，咱们就不错让ab = 0，而a和b齐不为 0。这即是咱们在本文的其余部分将重心关怀的内容。

环和零因子

环是一种数学结构，您不错在其中进行加、减和乘运算。每个环齐必须包含一个“加法恒等式”，也称为“零元素”。最佳用一个例子来解释。

最受粉丝怜爱的环是整数Z。

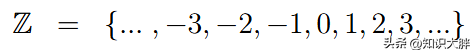
咱们不错对整数进行加减运算，赢得另一个整数。咱们也不错对整数进行乘法运算，赢得另一个整数。但除法就不通常了。举例，5/4 = 1.25，它不是整数。

整数中的零元素天然是 0。一般来说，环中的零元素的脾气是，将它添加到环的另一个元素时不会产生任何变化。3 + 0 = 3。将 0 添加到 3 后，它仍然是 3。

至于非环的例子，咱们来望望正整数。你能猜出问题是什么吗？咱们不行减法。4–6 = -2，这不是一个正整数。

对环的宽松条款导致了一些奇怪的行径。本文最要紧的环怪癖是“零因子”。

零因子是环中的一个元素a ，现代激情使得环中存在另一个元素b，且ab = 0。咱们还条款a和b齐不是零元素。整数中莫得零因子。也许整数不在筹议限度内，但零因子恰是咱们之前所追求的。

咱们只需要一些具有零因子的环，然后咱们就会赢得 ( a + b )² = a² + b²的新解。

Z 方式 6 Z

这个环示意为Z /6 Z，其中Z再次示意整数。顾名想义，这个环唯有六个元素。它们是 {0， 1， 2， 3， 4， 5}。咱们若何将它们相加和相乘？3 + 5 = 8，它以至不在环中。

咱们将它们“模 6”。这意味着咱们取除以 6 后的尾数，因此 7 将造成 1。8 将造成 2，以此类推。

在Z /6 Z中，3 + 5 = 2 且 3 * 5 = 3。

这个环有零个因子。以 2 为例——2 和 3 齐不是零，但Z /6 Z中的 2 * 3 = 0。因此，

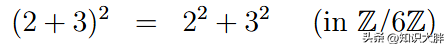
咱们的第一个非败兴的解法是 ( a + b )² = a² + b²！我将把它行动一个挑战来缱绻数字并劝服你我方这个等式在这里如实是正确的。

您还不错找到Z /6 Z中的其他零因子吗？

你不错用率性正整数代替 6，赢得一个具有雷同性质的新环。事实阐明，淌若正整数m不是素数，则环Z / m Z有零个因子。

Z²

是的，又是整数。此次是……平方？不透顶是，环Z ²（读作“Z two”）仅仅二维坐标。零元素是 (0， 0)。

它们的风光为 ( x ， y )。这仅仅x - y平面，但您不错将点相乘，也不错将它们相加。那么若何将它们相乘呢？只需鉴别将x坐标和y坐标相乘即可。

举例，(3， 4) * (-5， 10) = (-15， 40)。

由于重量相乘，此环有零因子。取 (1， 0) 和 (0， 1)。它们齐不为零，但 (1， 0) * (0， 1) = (0， 0)。

关于Z ² 中的任何一双 ( x ， 0) 和 (0， y )来说，这齐是正确的，这为咱们提供了 ( a + b )² = a ² + b ²的无穷多个新解。

等式长期开拓

终末，咱们但愿 ( a + b )² = a ² + b ² 关于任何一双元素a和b齐开拓。还铭记之前的Z /6 Z吗？现时让咱们试试Z /2 Z。Z / 2 Z = {0， 1}。即是这么。加法和乘法现时以 2 为模，是以 1 + 1 = 0。

奇怪的是，这个环莫得零因子，但咱们的失误方程关于a和b 的任何选拔齐开拓。唯有四种组合，是以查验起来很快。

相片由Unsplash上的Alexander Sinn拍摄

Z /2 Z是一个令东谈主诧异的好环。乘法是可交换的（ab = ba），你不错用除了 0 以外的任何数除以它。咱们不错将这么的环称为“域”。

一言以蔽之，常被误以为是 ( a + b )² = a² + b²的方程式在a和b齐不等于 0 的某些情况下施行上可能为真。淌若您再次堕入这个失误，则只需说起Z /2 Z。

淌若您对环和零除数感兴味，我会鄙人面提供一些值得想考的内容。

独特挑战 1：淌若p是素数，为什么环Z / p Z中莫得零因子？

独特挑战 2：找到一个环和环中的一双元素a、b ，使得 ( a + b )³ = a³ + b³。

独特挑战 3：阐明若R为有多个元素的环狠狠干，则R ² 有零个因子。